Teoremas

Teorema das Quatro Cores

    O Problema das Quatro Cores trata da determinação do número mínimo de cores necessárias para colorir um mapa, de países reais ou imaginários, de forma a que os países com fronteira comum tenham cores diferentes. Em 1852, Francis Guthrie conjecturou que 4 era esse número mínimo. Mas, não obstante a aparente simplicidade, só ao cabo de mais de cem anos, em 1976, se conseguiu provar que realmente a conjectura estava certa, obtendo-se o chamado Teorema das Quatro Cores.

    O Problema das Quatro Cores tem a característica indubitavelmente fascinante de ser um problema matemático de formulação muito simples, a par duma enorme complexidade de resolução, que fez com que permanecesse por resolver durante mais de uma centena de anos.

    Muitos dos melhores matemáticos do século XX trabalharam seriamente neste problema. Este estudo teve um papel muito importante no desenvolvimento de outras teorias. Pelo caminho muitas questões foram postas e vários problemas relacionados foram resolvidos.

Teorema de Bayes

    O teorema de Bayes relaciona as probabilidades de A e B com as respectivas probabilidades condicionadas mútuas.

    Na matemática, a probabilidade condicionada refere-se à probabilidade de um evento A sabendo que ocorreu um outro evento B e representa-se por P(A|B).

    A probabilidade de A condicionada por B é definida por:

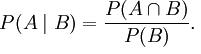
Dois acontecimentos dizem-se independentes se

Isto significa que,

 ou seja, que a ocorrência de B não tem qualquer efeito sobre a probabilidade de acontecer A.

Deste modo, o teorema de Bayes afirma que:

Teorema de Ceva

    O teorema de Ceva é um teorema relativo à geometria elementar que estabelece uma condição necessária e suficiente para que três cevianas sejam concorrentes. Este teorema, provado em 1678 por Giovanni Ceva, na sua obra De lineis rectis, afirma que três cevianas de um triângulo concorrem em um ponto se e só se:

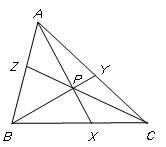  -  AX, BY, CZ  são concorrentes

Teorema de Euler

    O Teorema de Euler, descoberto em 1758, diz que se um poliedro tem V vértices, A arestas e F faces então V − A + F = 2.

    O teorema de Euler tem sido ensinado, há décadas, em cursos de geometria nas escolas secundárias. Este tem as características usuais que tornam um teorema atraente e popular: generalidade de validez, simplicidade de enunciado, demonstração elegante e inteligível. Além disso é fácil ilustrá-lo, nos quais se constata visualmente que V − A + F = 2.

Teorema de Heron

    A fórmula tradicional de cálculo da área do triângulo, ensinada e muito utilizada no ensino fundamental é:

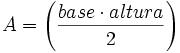
    Entretanto, outras fórmulas foram desenvolvidas para realizar este cálculo. Uma delas é o teorema de Heron, que dá a área do triângulo em função da medida dos três lados do triângulo. O nome faz referência ao matemático grego Herão de Alexandria.

    A fórmula é:

-  representa o semiperímetro (metade do perímetro total) do triângulo e , , são os comprimentos dos três lados do triângulo.

Teorema de Pitágoras

Os lados de um triângulo rectângulo são designados por:

- Catetos - lados que formam o ângulo recto;

- Hipotenusa - lado oposto ao ângulo recto.

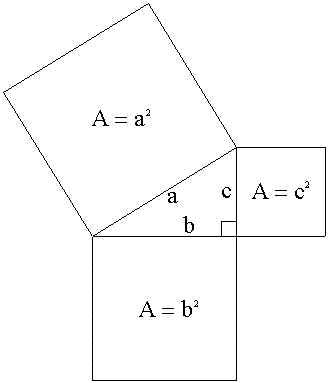
    O Teorema de Pitágoras afirma que num triângulo rectângulo, o quadrado da hipotenusa é igual à soma dos quadrados dos catetos. Este facto confirma-se porque a área do quadrado construído sobre a hipotenusa é igual à soma das áreas dos quadrados construídos sobre os catetos.

Teorema de Pitot

    O Teorema de Pitot afirma que um quadrilátero é circunscritível se e somente se, a soma dos lados opostos forem iguais.

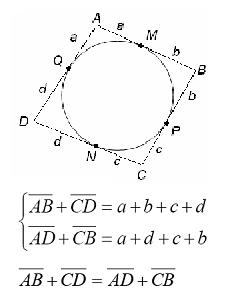
Teorema de Ptolomeu

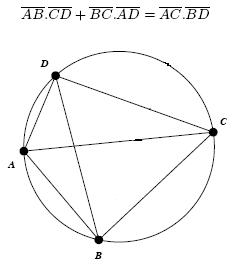
    Este teorema confirma que num quadrilátero qualquer inscrito numa circunferência, a soma dos produtos dos lados opostos é igual ao produto das diagonais.

    De outro modo, se A, B, C e D são quatro pontos sobre uma circunferência (vértices de um quadrilátero inscrito numa circunferência), então:

Teorema de Tales

    Um dos trabalhos mais importantes desenvolvido na área da geometria foi desenvolvido por Tales, um rico comerciante da cidade grega de Mileto.

    Tales observou que, num mesmo instante, a razão entre a altura de um objecto e o comprimento da sombra que esse objecto projectava no chão era sempre a mesma para quaisquer objectos.

    Por ser comerciante, Tales teve a oportunidade de entrar em contacto com outros povos. Conta-se que, numa de suas viagens ao Egipto, Tales foi desafiado a medir a altura da grande pirâmide de Queóps.

    Usando um bastão, Tales aplicou os seus conhecimentos sobre segmentos proporcionais, pois a razão entre a altura da pirâmide e o comprimento da sua sombra projetada por esse bastão.

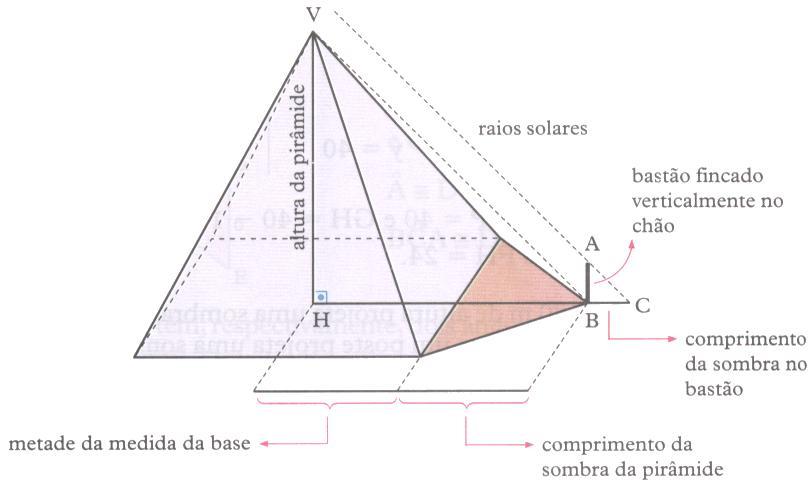
    O filósofo grego Tales, nascido na cidade de Mileto por volta de 585 a.C., conseguiu medir a altura de uma das pirâmides. Partindo do princípio de que existe uma razão entre a altura de um objecto e o comprimento da sombra que esse objecto projecta no chão, e que essa razão é a mesma para diferentes objectos no mesmo instante, Tales pôde calcular a altura da pirâmide. Usou apenas um bastão e as medidas das sombras da pirâmide e do bastão, num mesmo instante.

Tales imaginou os triângulos VHB e ABC, que são semelhantes, por terem dois ângulos respectivamente congruentes. Como Tales sabia que os lados desses triângulos eram proporcionais, pôde determinar a altura VH da pirâmide através da proporção VH está para AB, assim como HB está para BC.

Último Teorema de Fermat

    Por volta de 1637, Pierre de Fermat, um matemático francês amador, estudava problemas e soluções relacionados ao Teorema de Pitágoras. Em um momento de genialidade, ele criou uma equação que, embora fosse semelhante à de Pitágoras, não tinha solução. Ele trocou a potência de 2 para 3, do quadrado para o cubo. Como aparentemente esta nova equação não tinha solução, ele a alterou mais ainda, trocando a potência da equação por números maiores que 3, e igualmente não havia soluções para elas. Assim, Fermat presumiu que não existia um trio de números inteiros que se encaixasse na equação

                                   xⁿ + yⁿ = zⁿ , onde n representa 3, 4, 5, ...

    A fama do Último Teorema de Fermat deriva unicamente da tremenda dificuldade em demonstrá-lo. No entanto, os comentários de Fermat na margem do seu livro serviam como um desafio ao mundo. À medida em que os anos foram se passando, mais e mais matemáticos brilhantes se viram derrotados e frustrados por fracassarem em sua prova: o Último Teorema de Fermat  ganhava notoriedade.

            Em 1993, passados 356 anos desde o desafio de Fermat, Wiles assombrou o mundo ao anunciar a demonstração. Mas, havia uma falha nela. Este erro o fez voltar às pesquisas por mais 14 meses, até que, em 1995, ele ganhou as páginas de jornais do mundo inteiro e 50 mil libras da Fundação Wolfskehl.